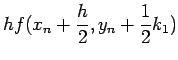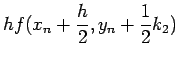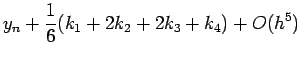Runge-Kutta 法

常微分方程式の数値解法で、オイラー法から修正オイラー法にすると 精度が劇的に改善した。より高精度な公式を使うと計算の能率はさらに上がる。 この中で古典的なものの１つは Runge-Kutta 法である。 4 次の Runge-Kutta 法

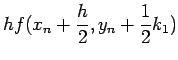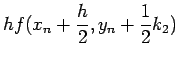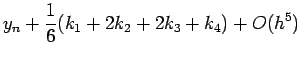$$k_1 = h f(x_n,y_n)$$

$$k_2 = h f(x_n + \frac{h}{2}, y_n +\frac{1}{2} k_1 )$$

$$k_3 = h f(x_n + \frac{h}{2}, y_n +\frac{1}{2} k_2 )$$

$$k_4 = h f(x_n + h, y_n + k_3 )$$

$$y_{n+1} = y_n +\frac{1}{6}(k_1 + 2 k_2 +2 k_3 + k_4) +O (h^5)$$ (1)

で、誤差は累積すると $O(h^4)$ である。中間値として4回 $f(x,y)$ を計算し なければならないが、精度の向上が著しいのでメリットがある。

Runge-Kutta 法の導出と、誤差の評価については 「工学のための応用数値計算法入門」 第8章3節 [1] など参照。

多元連立の常微分方程式に対しては、 $k_1,k_2,k_3,k_4$ を配列に置き換えれば良い。手続きは修正オイラー法の連立 常微分方程式の項も参考のこと。