do 構文による繰り返し

級数の和、数値積分と言った時には変数の値を少しづつ変えながら、同じ操作を 繰り返すことが必要になる。この場合に便利なのが do 構文によ る繰り返しである。

文法：

do $i=e1,e2,e3$

実行文の集合(do ブロック)

end do

$i:$ do 変数、$e1:$ 始値 $e2:$ 終値 $e3:$ 増分(全て整数型)。増分値は $e3=1$ の時、省略可。

最初は $i=e1$ として do ブロックを実行し、end do まで来た時、次の文を実 行するのではなく、最初の do 文のところに戻る。次に変数 $i$ の値を $e3$ だけ増やし($i = i+e3$)、再び do ブロックの実行を行なう。以下この操作を $i > e2$ となるまで繰り返す。終了条件に達すると、end do 文の次の実行文へ 移る。

例：

      integer n,n2
      real r1
c
      do n=1,10
         n2=n*n
         r1=1.0/n
         write(*,*) n,n2,r1
      end do
c
      end

例2：指数関数のテイラー展開

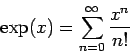$$\exp(x) = \sum_{n=0}^{\infty} \frac{x^n}{n!}$$ (1)

を最初の $m$ 項までの和をとり、近似する。

      real x,x1,sum
      integer n,max
c
      read(*,*) x,max
      sum=1.0
      x1=1.0
      do n=1,max
         x1=x1*x/n
         sum= sum + x1
      end do        
c
      write(*,*) sum,exp(x),sum/exp(x)
c
      end

例3：双曲線関数の無限乗積

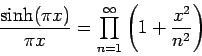$$\frac{\sinh ( \pi x )}{\pi x} = \prod_{n=1}^{\infty} \left(1+\frac{x^2}{n^2}\right)$$ (2)

の有限項での近似

      real x,pi,prod
      integer n,max
c
      pi = 4.0*atan(1.0)
      read(*,*) x,max
      prod=1.0
      do n=1,max
         prod= prod*(1.0+x*x/(n*n))
      end do        
c
      write(*,*) prod,sinh(pi*x)/(pi*x),prod/(sinh(pi*x)/(pi*x))
c
      end