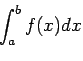 |
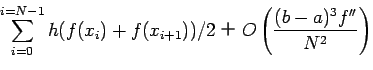 |
||
![$\displaystyle h \left[
\frac{1}{2} f(a) + \sum_{i=1}^{i=N-1} f(x_i)+\frac{1}{2} f(b) \right]
+O \left( \frac{(b-a)^3 f''}{N^2} \right),$](img4.png) |
|||
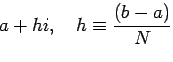 |
(1) |
微分とは異なり、一般に積分は解析的には求まらないので、 数値計算に頼る必要がでてくる。特異点のない場合、次の(閉じた) 台形公式により、数値積分ができる。
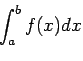 |
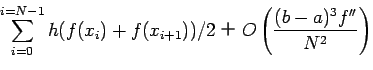 |
||
![$\displaystyle h \left[
\frac{1}{2} f(a) + \sum_{i=1}^{i=N-1} f(x_i)+\frac{1}{2} f(b) \right]
+O \left( \frac{(b-a)^3 f''}{N^2} \right),$](img4.png) |
|||
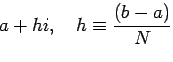 |
(1) |
![\includegraphics [height=5cm,clip]{fig5.eps}](img20.png)
[解説]
積分区間 ![]() を
を ![]() 等分し
等分し
![]() とし、、
各点での関数値を
とし、、
各点での関数値を
![]() で表す。
図のように関数
で表す。
図のように関数 ![]() を折れ線で近似すると、
各台形の面積は、
を折れ線で近似すると、
各台形の面積は、
![]() で、
(積分値
で、
(積分値 ![]() 台形の総面積) から上の台形公式が導ける。
台形の総面積) から上の台形公式が導ける。
課題1:
次の問題を数値積分して見よ。分割数![]() (刻み幅
(刻み幅 ![]() )に対する収束性を確認せ
よ。
)に対する収束性を確認せ
よ。
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |