

: Fortran 文法
: 数値計算法概論:No.9(ニュートン・ラフソン法)
: 数値計算法概論:No.9(ニュートン・ラフソン法)
任意の関数 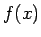 について、
について、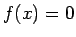 となる点
となる点 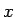 を求めよう。
図のように適当な初期値
を求めよう。
図のように適当な初期値 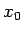 において
において 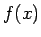 に接線を引けば、接線の方程式は
に接線を引けば、接線の方程式は
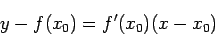 |
(1) |
であり、したがってこの接線と 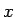 軸との交点
軸との交点 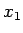 は
は 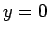 とおいて
とおいて
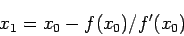 |
(2) |
で与えられる。
次に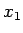 での
での 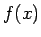 への接線と
への接線と 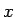 軸との交点を
軸との交点を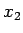 とする、という操
作を繰り返すと、交点は
とする、という操
作を繰り返すと、交点は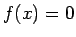 の解に近付く。
の解に近付く。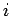 番目の繰り返しでは、
番目の繰り返しでは、
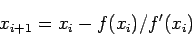 |
(3) |
になるので、適当な値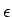 (収束半径) を決めておき、
(収束半径) を決めておき、
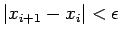 になったら、
になったら、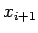 を解とみなす。
を解とみなす。
ニュートン法の収束は、2次収束
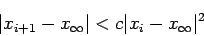 |
(4) |
で、真の値に近付くと極めて早い。大体、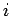 が1増えると有効桁数が倍になる。
が1増えると有効桁数が倍になる。
Kiyohide Nomura
平成15年6月25日
![]() について、
について、![]() となる点
となる点 ![]() を求めよう。
図のように適当な初期値
を求めよう。
図のように適当な初期値 ![]() において
において ![]() に接線を引けば、接線の方程式は
に接線を引けば、接線の方程式は
![\includegraphics[width=75mm]{fig9a.eps}](img9.png)
![]() での
での ![]() への接線と
への接線と ![]() 軸との交点を
軸との交点を![]() とする、という操
作を繰り返すと、交点は
とする、という操
作を繰り返すと、交点は![]() の解に近付く。
の解に近付く。![]() 番目の繰り返しでは、
番目の繰り返しでは、