

: 台形公式の精度向上法:Richardson 補外
: 数値積分の収束加速法
: Euler-Maclaurin 総和公式
分割数 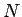 の時の台形公式による数値積分の結果を
の時の台形公式による数値積分の結果を 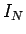 とする。
とする。
![\begin{displaymath}
I_N = h_N \left[\frac{1}{2} f(a) + \sum_{i=1}^{i=N-1} f( a + h_N i)
+\frac{1}{2}f(b) \right] ; \;
h_{N} = \frac{b-a}{N}
\end{displaymath}](img16.png) |
(4) |
台形公式の収束性はオイラー・マクローリンの公式(1)
で与えられ、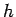 の偶関数で
ある。分割数
の偶関数で
ある。分割数 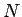 に対して誤差は
に対して誤差は
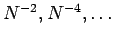 と振舞う。
と振舞う。
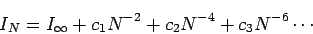 |
(5) |
ところで 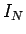 と
と 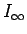 の直接比較して収束性評価できるのは結果が解
析的に分かっている場合のみである。
一般には、
の直接比較して収束性評価できるのは結果が解
析的に分かっている場合のみである。
一般には、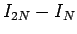 を調べることで
収束性を調べられる。例えば誤差が、
を調べることで
収束性を調べられる。例えば誤差が、
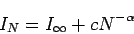 |
(6) |
と冪乗的に振舞うなら、
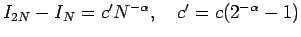 となる。
さらに
となる。
さらに
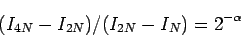 |
(7) |
として誤差の収束の早さも評価できる。
Kiyohide Nomura
平成15年6月6日
![]() の時の台形公式による数値積分の結果を
の時の台形公式による数値積分の結果を ![]() とする。
とする。
![\begin{displaymath}
I_N = h_N \left[\frac{1}{2} f(a) + \sum_{i=1}^{i=N-1} f( a + h_N i)
+\frac{1}{2}f(b) \right] ; \;
h_{N} = \frac{b-a}{N}
\end{displaymath}](img16.png)
![]() と
と ![]() の直接比較して収束性評価できるのは結果が解
析的に分かっている場合のみである。
一般には、
の直接比較して収束性評価できるのは結果が解
析的に分かっている場合のみである。
一般には、![]() を調べることで
収束性を調べられる。例えば誤差が、
を調べることで
収束性を調べられる。例えば誤差が、