

: レポート
: 収束加速法:Aitken 法
: 交代級数
1次収束と、
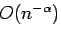 の両者が混合したケース
の両者が混合したケース
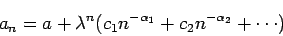 |
(4) |
(ここで
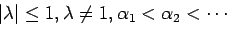 であ
る。
であ
る。
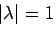 の場合はさらに
の場合はさらに
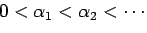 とする)の
数列に対して No.1 の (17) 式のように Aitken 加速すると、
とする)の
数列に対して No.1 の (17) 式のように Aitken 加速すると、
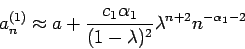 |
(5) |
となる[1](ただし、
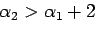 を前提とし
ている)。混合型を Aitken 加速した結果は再び混合型になっているので、さら
に Aitken 加速することが可能である。
交代数列は、
を前提とし
ている)。混合型を Aitken 加速した結果は再び混合型になっているので、さら
に Aitken 加速することが可能である。
交代数列は、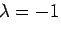 の場合に当たる。
式 (
の場合に当たる。
式 (![[*]](crossref.png) ) の導出は面倒であるので付録で紹介する。
) の導出は面倒であるので付録で紹介する。
Kiyohide Nomura
平成17年6月6日
![]() の両者が混合したケース
の両者が混合したケース
![[*]](crossref.png) ) の導出は面倒であるので付録で紹介する。
) の導出は面倒であるので付録で紹介する。