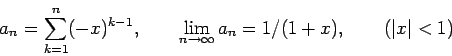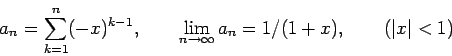

: 期限、提出先など
: レポート
: レポート
- 以下の級数
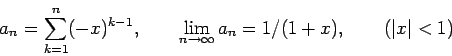 |
(6) |
を Aitken 加速してみよ(1回で十分のはずである)。
これは1次収束である。No.1 の 2.2.2 の (16) 式を使い、収束性を調べてみよ。
- 交代級数(今回のプリントの (1),(2) その他岩波数学公式集 II p。37 など参照)
の内1つ以上の Aitken 加速をして見よ。
- 数値積分の台形公式で区間の端で被積分関
数が
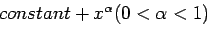 と振舞う時、誤差は
と振舞う時、誤差は
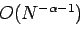 程度である(解析的に導いて見よ)。この
場合も分割数を2の冪乗にとると Aitken 加速が使える。
以前扱った関数の台形公式による積分で、
程度である(解析的に導いて見よ)。この
場合も分割数を2の冪乗にとると Aitken 加速が使える。
以前扱った関数の台形公式による積分で、
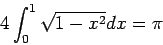 |
(7) |
の収束性を調べ、Aitken 加速してみよ。
余裕があれば
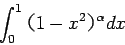 |
(8) |
と一般化したものについても調べよ。
Kiyohide Nomura
平成17年6月6日