

: その他の収束加速法
: 計算物理学:No.3
: 収束加速法:Aitken 法
混合型の収束列
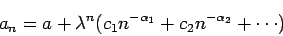 |
(1) |
で 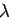 が既知の場合、Richardson 加速が実行でき、
が既知の場合、Richardson 加速が実行でき、
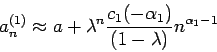 |
(2) |
となる(これを確かめてみよ)
[1]
。従って再び混合型となり、Richardson 加速を
繰返し適応できる。
交代数列は混合型
の 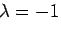 の場合にあたるので、
交代数列に対し
の場合にあたるので、
交代数列に対し
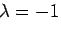 とした Richardson 加速も実行できる。余裕があれば、レポート課題の
交代数列にたいして、Richardson 加速を試してみよ。
とした Richardson 加速も実行できる。余裕があれば、レポート課題の
交代数列にたいして、Richardson 加速を試してみよ。
Kiyohide Nomura
平成17年6月6日
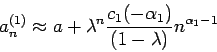
![]() の場合にあたるので、
交代数列に対し
の場合にあたるので、
交代数列に対し
![]() とした Richardson 加速も実行できる。余裕があれば、レポート課題の
交代数列にたいして、Richardson 加速を試してみよ。
とした Richardson 加速も実行できる。余裕があれば、レポート課題の
交代数列にたいして、Richardson 加速を試してみよ。