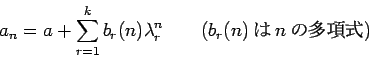

: 参考文献
: その他の収束加速法
: その他の収束加速法
 -algorithm の手続きは、以下の通りである。
-algorithm の手続きは、以下の通りである。
1) 2 次元配列  を用意し、その第0行に元の配列を入れる。
を用意し、その第0行に元の配列を入れる。
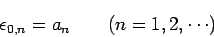 |
(4) |
2) 隣の要素との差の逆数を次の行に書く。
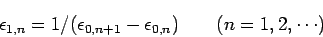 |
(5) |
3)
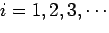 の順に
の順に
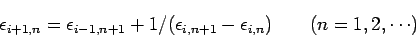 |
(6) |
このようにして得られた
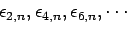 が収束加速列である。
が収束加速列である。
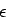 -algorithm は特に
-algorithm は特に
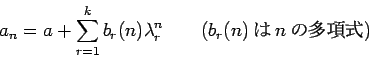 |
(7) |
という場合には、
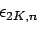 (
(
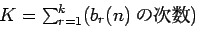 )
が正しい収束値
)
が正しい収束値 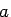 を与える。
を与える。
Kiyohide Nomura
平成17年6月6日
![]() -algorithm の手続きは、以下の通りである。
-algorithm の手続きは、以下の通りである。
![]() を用意し、その第0行に元の配列を入れる。
を用意し、その第0行に元の配列を入れる。
![]() -algorithm は特に
-algorithm は特に