

: Euler 法
: 常微分方程式の数値解法
: 常微分方程式の数値解法
常微分方程式の問題は、常に1階の微分方程式の組に置き換えることができる。
例えば、2階の微分方程式
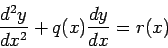 |
(1) |
は新しい変数 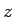 を補助的に用いて、連立の1階微分方程式
を補助的に用いて、連立の1階微分方程式
に書き直すことができる。
一般に(多変数、高階の)常微分方程式の問題は、関数
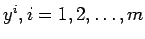 に対して、
に対して、
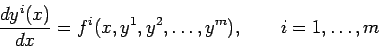 |
(3) |
の正規形をした 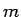 元連立1階微分方程式に帰着する。
初期条件
元連立1階微分方程式に帰着する。
初期条件 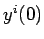 の組を与えると、これを数値的に解くことができる。
の組を与えると、これを数値的に解くことができる。
Kiyohide Nomura
平成17年6月6日
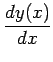
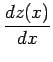
![]() に対して、
に対して、