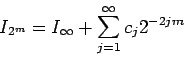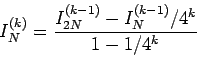

: プログラム
: 数値積分の収束加速法
: 収束性
さらにオイラー・マクローリンの公式
(1)
を使うと収束性を改善できる。つまり、
と
を比較して、
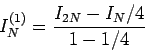 |
(8) |
とすると 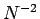 の誤差の項が打ち消されるので、
の誤差の項が打ち消されるので、
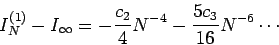 |
(9) |
となり元の 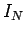 より収束が早くなる。この操作を Richardson 加速
[3,4]と呼ぶ。台形公式による数
値積分を Richardson 加速すると、誤差は一般に
より収束が早くなる。この操作を Richardson 加速
[3,4]と呼ぶ。台形公式による数
値積分を Richardson 加速すると、誤差は一般に 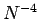 のように振舞う。
のように振舞う。
上のようにして得られた 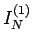 の数列を、さらに
の数列を、さらに
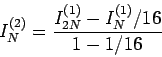 |
(10) |
とすると、誤差が 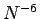 のように振舞う。
のように振舞う。
特に分割数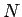 を
を
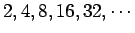 と2の冪乗
と2の冪乗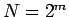 にとると、
にとると、
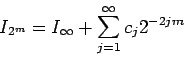 |
(11) |
であるので、上の操作を繰り返すことができて、
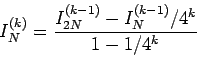 |
(12) |
とするとさらに収束を早くできる。
Kiyohide Nomura
平成15年6月6日
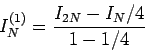
![]() の数列を、さらに
の数列を、さらに
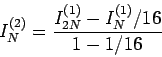
![]() を
を
![]() と2の冪乗
と2の冪乗![]() にとると、
にとると、