

: ユーザー受信機の誤差を考えた場合
: GPS 測位の原理
: GPS 測位の原理
まず、GPS 衛星とユーザー受信機ともに正確な時計を共有している場合を考えま
しょう。
この時、ある GPS 衛星から電波を送信した時刻
![$t_{t} {\rm [ sec]}$](img5.png) と、ユーザー受信機で受信した時刻
と、ユーザー受信機で受信した時刻
![$t_{r} {\rm [ sec]}$](img6.png) を測定すれば、その間の距離
を測定すれば、その間の距離
![$r {\rm [m]}$](img7.png) は光速
は光速
![$c {\rm [m/sec]}$](img8.png) を使って
を使って
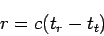 |
(2) |
により求めることができます。
次に複数の GPS 衛星(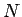 個)を考え、
個)を考え、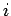 番目の GPS 衛星とユーザ受信機の間
の測定距離を
番目の GPS 衛星とユーザ受信機の間
の測定距離を
![$r_{i} {\rm [m]}$](img12.png) とします。GPS 衛星の位置はわかっているものとしてユーザ受信機の位置を求め
ることを考えます。
ユーザー受信機位置を
とします。GPS 衛星の位置はわかっているものとしてユーザ受信機の位置を求め
ることを考えます。
ユーザー受信機位置を
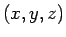 、
、
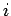 番目の GPS 衛星の位置を
番目の GPS 衛星の位置を
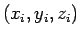 とすると、
とすると、
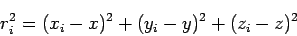 |
(3) |
したがって、ユーザー受信機位置を求めるには
の連立方程式を 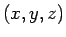 について解けば良いわけです。
これは平面図で表すと、図
2
のように、各送信源を中心とする円の交点として位置を求めることに当
たります。
について解けば良いわけです。
これは平面図で表すと、図
2
のように、各送信源を中心とする円の交点として位置を求めることに当
たります。
Kiyohide NOMURA
平成21年6月10日
![]() 個)を考え、
個)を考え、![]() 番目の GPS 衛星とユーザ受信機の間
の測定距離を
番目の GPS 衛星とユーザ受信機の間
の測定距離を
![]() とします。GPS 衛星の位置はわかっているものとしてユーザ受信機の位置を求め
ることを考えます。
ユーザー受信機位置を
とします。GPS 衛星の位置はわかっているものとしてユーザ受信機の位置を求め
ることを考えます。
ユーザー受信機位置を
![]() 、
、
![]() 番目の GPS 衛星の位置を
番目の GPS 衛星の位置を
![]() とすると、
とすると、