ユーザー受信機の誤差を考えた場合

次にユーザー受信機の時計に誤差がある場合を考えます。 実際、GPS 衛星には高精度の原子時計が搭載されているのに対して、ユーザー受 信機には原子時計より精度は落ちますが、ずっと安価で取扱の容易な水晶時 計を使っています。

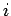$i$ 番目の GPS 衛 星とユーザ受信機の正確な距離を $r_i {\rm [m]}$、 受信機の時計の進みを $\delta {\rm [sec]}$ 、 受信機の時計誤差を含む測定時間差から求めた疑似距離(pseudo-range)を $r'_{i}{\rm [m]}$ とするとその間の関係は

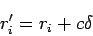$$r'_{i} = r_{i} + c \delta$$ (5)

となります。 この場合はユーザー受信機位置を求めるには

$$(r'_{1}- c\delta)^2 = (x_{1}-x)^2+ (y_{1}-y)^2 +(z_{1}-z)^2$$

$$(r'_{2}-c \delta)^2 = (x_{2}-x)^2+ (y_{2}-y)^2 +(z_{2}-z)^2$$

$$\cdots$$

$$(r_{N}-c\delta)^2 = (x_{N}-x)^2+ (y_{N}-y)^2 +(z_{N}-z)^2$$ (6)

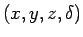の連立方程式を $(x,y,z,\delta)$ について解けば良いわけです。 未知数が4つですので、最低4つ以上の方程式、つまり4つ以上の GPS 衛星のデー タが必要です。

より多くのGPS 衛星のデータが利用できれば、より精度の高い位置情報を得るこ とができます。