修正 Euler 法

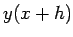$y(x+h)$ の厳密な値は、積分を用いて

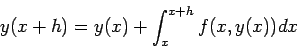$$y(x+h) = y(x) + \int_{x}^{x+h} f(x,y(x)) dx$$ (1)

と表すことができる。オイラー法は、この積分を

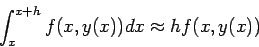$$\int_{x}^{x+h} f(x,y(x)) dx \approx h f(x,y(x))$$ (2)

で近似すること(図 1-a) に相当するが、離散近似による誤差をもっと小さくする ためには、台形公式を用いて、

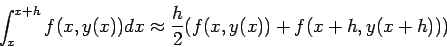$$\int_{x}^{x+h} f(x,y(x)) dx \approx \frac{h}{2}( f(x,y(x)) + f (x+h, y(x+h)))$$ (3)

で近似する(図 1-b)。

図: (a) オイラー法 (b) 修正オイラー法 (c) 2次のルンゲクッタ法に相 当。

しかし、微分方程式の計算の場合には数値積分と違い、被積分関数の中に 未知関数があり、() の右辺には左辺で予測すべき量 が含まれている。

そこで、まずオイラー法で 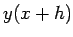$y(x+h)$ の近似値

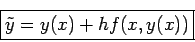$$\fbox{$ \tilde{y} = y(x) + h f (x,y(x)) $}$$ (4)

を計算し、それを() の右辺に代入する

$$\fbox{$ y (x+h) = y(x) + \frac{h}{2} \left[ f (x,y(x))+ f (x+h,\tilde{y}) \right] $}$$ (5)

これが修正オイラー法である。