BKT 転移で ![]() 対称性の破れを伴うものを sine-Gordon モデルで表す.
式 (12) で
対称性の破れを伴うものを sine-Gordon モデルで表す.
式 (12) で ![]() の項を
の項を
![]() とおきかえ,
とおきかえ,
![]() とする(この場合,
とする(この場合,![]() での双対性は
での双対性は
![]() ).
).
Massive 領域では
![]() へ繰り込まれ,
へ繰り込まれ,
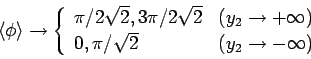 |
(20) |
前節の量子数の他,![]() が奇数・偶数にも物理的意味が出る(量子スピン系の波
数
が奇数・偶数にも物理的意味が出る(量子スピン系の波
数 ![]() に対応).
に対応).
![]() は
は![]() で同じスケーリング次元
で同じスケーリング次元 ![]() を持つが,
を持つが,
![]() で sine-Gordon モデルの
で sine-Gordon モデルの ![]() の相互作用項によりパリティの
違う2状態間の分裂が起こる
(表 2)
[15,14].
なお,BKT 転移線上では励起の構造が triplet-singlet と SU(2)
対称性と関連し,対数補正も
の相互作用項によりパリティの
違う2状態間の分裂が起こる
(表 2)
[15,14].
なお,BKT 転移線上では励起の構造が triplet-singlet と SU(2)
対称性と関連し,対数補正も ![]() と Clebsch-Gordan 係数と一
致する.
と Clebsch-Gordan 係数と一
致する.