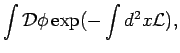 |
|||
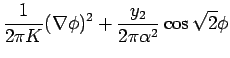 |
(12) |
2次元古典系,1次元量子系の多様な系が BKT 転移を示すが,個 別に扱うと繁雑なので,ボゾン化などで sine-Gordon ・2次元クーロンガス といった有効モデルに置き換え[3,19,20],繰り込 み群的解析をする.
1+1 次元量子 sine-Gordon 模型は
| (13) |
まず自由場(![]() )の相関関数を調べる.
)の相関関数を調べる.
![]() の相関関数は
の相関関数は
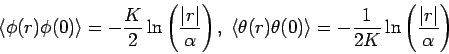 |
(14) |
| (15) |
| (16) |
![\begin{displaymath}
\langle O_{m,n}(r)O_{-m,-n}(0) \rangle
= \exp \left[ - 2 ...
...m,n} \Theta \right], \;
r \equiv \vert r\vert \exp (i \Theta)
\end{displaymath}](img163.png) |
(17) |
次に相互作用のある場合 ![]() に進もう.
摂動論的繰り込み群で扱うと,
に進もう.
摂動論的繰り込み群で扱うと,![]() として
式(5)が得られ,
として
式(5)が得られ,![]() の前後で
の前後で
![]() 項が relevant から irrelevant に変わる.
この時,双対性は成立しない
が,スケーリング次元の交差は BKT 臨界線の判定に使えるのではないか?
実際,繰り込み群からスケーリング次元への有限サイズ補正を求め
ると表 1 となり,BKT 転移点
項が relevant から irrelevant に変わる.
この時,双対性は成立しない
が,スケーリング次元の交差は BKT 臨界線の判定に使えるのではないか?
実際,繰り込み群からスケーリング次元への有限サイズ補正を求め
ると表 1 となり,BKT 転移点 ![]() で対数補正を
含めても (
で対数補正を
含めても (
![]() ) と (
) と (![]() )の励起が交差する.
)の励起が交差する.
量子数については ![]() で
で ![]() は U(1) 対称性を失い量子数
は U(1) 対称性を失い量子数 ![]() は無意味になるが,
は無意味になるが,
![]() の反転で不変なためパリティの量子数が残る.
演算子の側でもこれを考慮し,
の反転で不変なためパリティの量子数が残る.
演算子の側でもこれを考慮し,
![]() という形のものをとる.
という形のものをとる.
演算子の繰り込みについては ![]() が式
(5) で繰り込まれ,(18) から
スケーリング次元全体に影響する.
さらに
が式
(5) で繰り込まれ,(18) から
スケーリング次元全体に影響する.
さらに
![]() とマージナル演算子は
とマージナル演算子は ![]() の繰り込みの影響
も受ける.
これは
の繰り込みの影響
も受ける.
これは ![]() でスケーリング次元が
同じになるだけでなく,対称性(量子数)
でも U(1)・パリティ・波数全て同じなので,
sine-Gordon モデルの
でスケーリング次元が
同じになるだけでなく,対称性(量子数)
でも U(1)・パリティ・波数全て同じなので,
sine-Gordon モデルの ![]() の相互作用項により2状態間の混成が起こるからで
ある.以上をまとめたものが前出の表 1 である.
の相互作用項により2状態間の混成が起こるからで
ある.以上をまとめたものが前出の表 1 である.
では繰り込み群の高次ではどうか?
実は sine-Gordon 模型の BKT 転移
線が SU(2) Thirring モデルにマップできる性質 [22]を反映し,繰
り込み群の高次でもスケーリング次元の構造は変わらない.
今のケースでは BKT 転移線上の SU(2) 対称性は間接的だったが,
次節の massive 領域で ![]() 対称性の破れがあるケースでは SU(2) 対
称性があらわに出る.
対称性の破れがあるケースでは SU(2) 対
称性があらわに出る.