
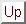

: 電子系
: 具体例
: スピン系(S=1/2; 対称性)
次にボンド交替のある XXZ スピン鎖
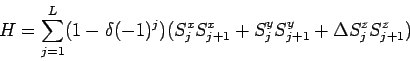 |
(24) |
を例にとる.これは,スピンパイエルス転移で重要であるし,
もともと相互作用が交替的な物質もある.
この系で S=1の場合,臨界的(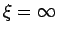 )な XY 相
と,massive な Haldane,dimer 相がある
[26,17].
前節と異なり Haldane相,dimer 相には対称性の破れ
がない.従って XY-Haldane,dimer 相の転移は
)な XY 相
と,massive な Haldane,dimer 相がある
[26,17].
前節と異なり Haldane相,dimer 相には対称性の破れ
がない.従って XY-Haldane,dimer 相の転移は 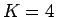 BKT 転移に当たる.
BKT 転移に当たる.
この場合,ハミルトニアン(24) で
量子数(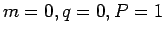 )の第1励起と,(
)の第1励起と,(
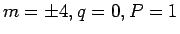 )の最低励起
の交差から BKT 転移線が決められる(図 6).
注目すべきことに,XY-Haldane の相境界はちょうど
)の最低励起
の交差から BKT 転移線が決められる(図 6).
注目すべきことに,XY-Haldane の相境界はちょうど 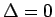 であるが,こ
れについて納得できる説明はまだない.
であるが,こ
れについて納得できる説明はまだない.
図 6:
S=1 のボンド交替鎖の相図.XY-dimer,XY-Haldane は BKT 転移,
dimer-Haldane はガウシアン転移,Néel の相境界は2次元イジングタイプ
のユニバーサリティークラス
([17] Fig.1 より転載).
 |
さらに,量子数(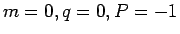 )の励起と量子数(
)の励起と量子数(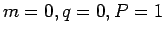 )の第2
励起があるが,これらに対する対数補正の寄与は BKT 転移線上で
)の第2
励起があるが,これらに対する対数補正の寄与は BKT 転移線上で
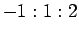 なので励起スペクトルの情報から対数補正を打ち消しス
ケーリング次元を求めることができる(図 7).
なので励起スペクトルの情報から対数補正を打ち消しス
ケーリング次元を求めることができる(図 7).
図 7:
BKT 転移線上でのスケーリング次元.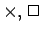 : 裸のスケーリ
ング次元,
: 裸のスケーリ
ング次元,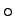 : 対数補正取り除いたスケーリング次元
([17] Fig.4 より転載).
: 対数補正取り除いたスケーリング次元
([17] Fig.4 より転載).
 |
Kiyohide Nomura
平成16年6月8日
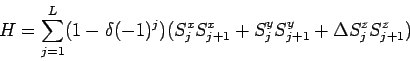
![]() )の第1励起と,(
)の第1励起と,(
![]() )の最低励起
の交差から BKT 転移線が決められる(図 6).
注目すべきことに,XY-Haldane の相境界はちょうど
)の最低励起
の交差から BKT 転移線が決められる(図 6).
注目すべきことに,XY-Haldane の相境界はちょうど ![]() であるが,こ
れについて納得できる説明はまだない.
であるが,こ
れについて納得できる説明はまだない.

![]() )の励起と量子数(
)の励起と量子数(![]() )の第2
励起があるが,これらに対する対数補正の寄与は BKT 転移線上で
)の第2
励起があるが,これらに対する対数補正の寄与は BKT 転移線上で
![]() なので励起スペクトルの情報から対数補正を打ち消しス
ケーリング次元を求めることができる(図 7).
なので励起スペクトルの情報から対数補正を打ち消しス
ケーリング次元を求めることができる(図 7).