![[*]](crossref.png) ) 式から、
) 式から、
実際の問題では収束率![]() が未知であることが多い。そのような場合、
(
が未知であることが多い。そのような場合、
(![[*]](crossref.png) ) 式から、
) 式から、
| (15) |
| (16) |
この ![]() の推定式をRichardson 補外で導いた式 (
の推定式をRichardson 補外で導いた式 (![[*]](crossref.png) )
に代入すると、
)
に代入すると、
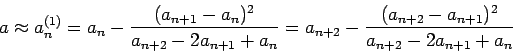 |
(17) |
Aitken 加速は1次収束に対してだけでなく、
混合型 (![[*]](crossref.png) ) や交代的な収束性を示すもの
(
) や交代的な収束性を示すもの
(![[*]](crossref.png) ) にも有効である
(説明は次回以降)。
しかし、単純な冪乗的収束を示すもの(
) にも有効である
(説明は次回以降)。
しかし、単純な冪乗的収束を示すもの(![[*]](crossref.png) )には、あまり効果がない。
)には、あまり効果がない。
得られた数列 ![]() に対し、Aitken 加速をさらに繰り
返し、
に対し、Aitken 加速をさらに繰り
返し、
![]() と収束を向上できる。
と収束を向上できる。
課題:
与えられた数列に対し、Aitken 加速された数列を返すプログラムを(で きればサブルーチンの形で)作れ。倍精度実数を使うこと。