

: 対称性の破れを伴う BKT 転移
: レベルスペクトロスコピー
: レベルスペクトロスコピー
通常の BKT 転移では massive 相に対称性の破れがない.
表 1 にスケーリング次元(励起と (6) で関連)
と量子数の対応をまとめた[12].
Marginal なスケーリング次元 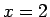 付近を調べると,
BKT 転移線
付近を調べると,
BKT 転移線
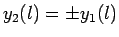 で,量子数(
で,量子数(
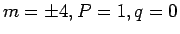 )と
(
)と
(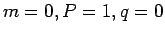 )の励起が交差する
(表 1,図 2)ので,これから転移線を決定できる.
次に BKT 転移線上での対数補正(
)の励起が交差する
(表 1,図 2)ので,これから転移線を決定できる.
次に BKT 転移線上での対数補正(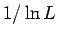 )の比が
)の比が
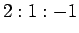 (表1の
(表1の
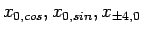 に対応)を使い対数補正を除去し,ユニバーサリティークラスを確認できる.
に対応)を使い対数補正を除去し,ユニバーサリティークラスを確認できる.
BKT 転移線での励起準位交差は,実は(隠れた) SU(2) 対称性を反映しており,
対数補正の高次の項まで成立している.
図 2:
BKT 転移線近傍のスケーリング次元 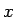
![\includegraphics[width=5cm]{scaling2.eps}](img94.png) |
表 1:
量子数(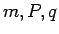 )と繰り込まれたスケーリング次元
)と繰り込まれたスケーリング次元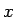 .BC は境界条件の分類を
表し,PBC は周期的境界,TBC はひねり境界である(TBC でのパリ
ティは PBC と異なるので,
.BC は境界条件の分類を
表し,PBC は周期的境界,TBC はひねり境界である(TBC でのパリ
ティは PBC と異なるので,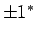 と区別した).
と区別した).
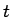 は BKT 転移点からの
距離(
は BKT 転移点からの
距離(
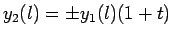 ).
).
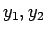 は繰り込み群方程式
(5)に従い,BKT 転移線上で
は繰り込み群方程式
(5)に従い,BKT 転移線上で
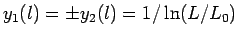 .
.
| m |
P |
q |
BC |
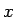 |
operator in s.G. |
apprev. |
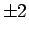 |
1 |
0 |
PBC |
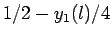 |
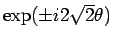 |
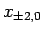 |
| 0 |
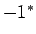 |
|
TBC |
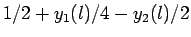 |
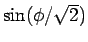 |
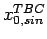 |
| 0 |
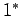 |
|
TBC |
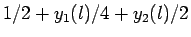 |
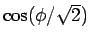 |
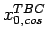 |
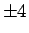 |
1 |
0 |
PBC |
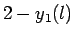 |
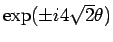 |
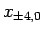 |
| 0 |
1 |
0 |
PBC |
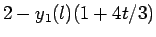 |
marginal |
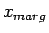 |
| 0 |
-1 |
0 |
PBC |
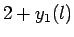 |
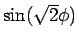 |
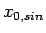 |
| 0 |
1 |
0 |
PBC |
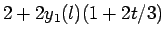 |
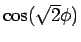 |
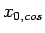 |
|


: 対称性の破れを伴う BKT 転移
: レベルスペクトロスコピー
: レベルスペクトロスコピー
Kiyohide Nomura
平成16年6月8日
![]() 付近を調べると,
BKT 転移線
付近を調べると,
BKT 転移線
![]() で,量子数(
で,量子数(
![]() )と
(
)と
(![]() )の励起が交差する
(表 1,図 2)ので,これから転移線を決定できる.
次に BKT 転移線上での対数補正(
)の励起が交差する
(表 1,図 2)ので,これから転移線を決定できる.
次に BKT 転移線上での対数補正(![]() )の比が
)の比が
![]() (表1の
(表1の
![]() に対応)を使い対数補正を除去し,ユニバーサリティークラスを確認できる.
に対応)を使い対数補正を除去し,ユニバーサリティークラスを確認できる.