

: 通常の BKT 転移
: BKT 転移とレベルスペクトロスコピー
: BKT 転移と2次転移
本節では BKT 転移の困難を解決したレベルスペクトロスコピー
を紹介する.
BKT転移のスケーリング次元の構造を調べると
BKT転移線で irrelevantから relevant へ,又はその逆になるものがあるので,
スケーリング次元の交差から転移点を決定し,対数補正を除
去できる[12].
1次元量子系の場合,長さ 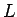 の有限系で周期境界条件(PBC)の下で,励起エネルギー
の有限系で周期境界条件(PBC)の下で,励起エネルギー
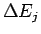 とスケーリング次元
とスケーリング次元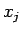 との関係は[6]
との関係は[6]
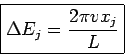 |
(6) |
(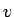 は電子系のフェルミ速度,または量子スピン系のスピン波速度)なので,
励起スペクトルからスケーリング次元を調べることができる.
は電子系のフェルミ速度,または量子スピン系のスピン波速度)なので,
励起スペクトルからスケーリング次元を調べることができる.
さらに各励起は量子数(例えば磁化・電子密度等の量子数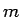 (U(1) 対称性),
パリティ
(U(1) 対称性),
パリティ 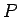 (空間反転),波数
(空間反転),波数 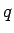 )で分類できる.
)で分類できる.
ところで,BKT 転移には離散的対称性の破れを伴う場合
もあり,同じ繰り込み群方程式で記述されるが,臨界指数
は異なる.
レベルスペクトロスコピーを使う際の手順を以下に示す.
- 離散的対称性の破れの有無による分類
- 離散的対称性の破れのない場合 [12,13]
3.1,3.3 節の説明と表 1 から量子数
と励起の対応をとり,準位交差から BKT・ガウシアン
転移線決定
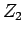 離散的対称性の破れを伴う場合 [14]
離散的対称性の破れを伴う場合 [14]
3.2 節の説明と表 2 から量子数と励起の
対応をとり,準位交差から BKT・ガウシアン転移線
決定
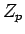 (
(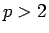 の整数)対称性の破れを伴う場合
の整数)対称性の破れを伴う場合
本解説では取り上げていないが,文献 [12] で考察.
クロックモデル,多重ウムクラップ過程などに関連
- ユニバーサリティークラスの確認(対数補正の除去)
- スケーリング次元
表 1,2 から
対数補正が打ち消し合う組合せをとり,スケーリング次元が予想
と合うか確認(3.4 節)
- セントラルチャージ
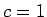 の確認(3.5 節)
の確認(3.5 節)
レベルスペクトロスコピーは対数補正を打ち消す組合せをとっているので,小さ
な系の数値計算でも無限系に非常に近い結果になる
(実際には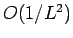 の補正が残るが,十分収束早い).
の補正が残るが,十分収束早い).
Kiyohide Nomura
平成16年6月8日
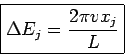
![]() (U(1) 対称性),
パリティ
(U(1) 対称性),
パリティ ![]() (空間反転),波数
(空間反転),波数 ![]() )で分類できる.
)で分類できる.
![]() の補正が残るが,十分収束早い).
の補正が残るが,十分収束早い).